Vector Databases: A New Dimension in Data Storage

23 September 2024 | 8 min

One of the key innovations in AI is the ability of models to create vector embeddings that capture the semantic meaning of unstructured data. These embeddings are used in a wide range of applications, from natural language processing to image recognition. However, storing and querying these embeddings efficiently is a challenging problem. Traditional databases are not optimised for high-dimensional data, and as a result, can be slow and inefficient when working with embeddings.

Enter vector databases. Vector databases are a new class of database specifically designed efficiently to store and query high-dimensional data. In this blog post, we will explore how vector databases work, and why they are a game-changer for AI applications.

1. What Do Vector Databases Do?

Almost all vector database use cases can be boiled down to the same task: storing high-dimensional embeddings for similarity queries. Unlike traditional databases, where queries tend to be based on exact matches or range queries, vector database queries are usually based on similarity. Typical vector database queries include finding the most similar embeddings to a given query embedding or finding embeddings that are similar to a set of query embeddings.

This ability to query based on similarity is incredibly powerful for information retrieval but is not that useful on its own. To make this capability truly useful, vector databases also store metadata alongside the embeddings. This metadata can be used to filter the results of a query or to provide additional context to the embeddings, such as the source of the original unembedded data.

To demonstrate how this is useful, consider the example of a vector database powering a document search engine:

1. Use an AI model, such as an LLM, to generate embeddings for each document in the corpus.
2. Store these embeddings in a vector database, along with metadata such as the document title and author.
3. When a user enters a search query, generate an embedding for the query using the same AI model.
4. Query the vector database for the most similar embeddings (representing documents) to the query embedding (representing the user's search).
5. Return the metadata for the most similar document embeddings as search results.

2. How Do Vector Databases Work?

Now that we know what vector databases do, the next question is how do they do it?

1. Similarity Metrics

The first piece of the puzzle is what does it mean to be similar? In the context of vector databases, similarity is usually measured using the choice of a number of metrics. The choice of similarity metric is usually up to the user and depends on the specific use case. A general rule of thumb is to use the similarity metric that best matches the metric used to train your embedding model. Some common similarity metrics include:

• L2 or Euclidean Distance
  Euclidean distance is probably the most intuitive of the metrics, it is simply the straight line distance between two vectors.

• Cosine Similarity
  Cosine similarity measures the angle between two vectors. This does not take the magnitude of the vector into account. It is useful for measuring semantic similarity, as it can find vectors pointing in the same semantic direction (regardless of magnitude).

• Inner Product
  The inner product is the projection of one vector onto another and takes into account both magnitude and direction. If the magnitudes of the vectors are normalised, it is equivalent to cosine similarity, but it is faster to compute than cosine similarity.

There are some other similarity metrics that can be used such as Jaccard distance and Hamming distance, which both operate on binary data, but these are less common.

2. Nearest Neighbour Search

Once we have chosen a similarity metric, the next problem to solve is how to efficiently find the most similar embeddings to a given query embedding. The most common approach to this problem is to use a k-nearest neighbour (KNN) search. This involves finding the k embeddings in the database that are closest to the query embedding according to the chosen similarity metric. The problem with this is that it requires computing the distance between the query embedding and every embedding in the database, which can be computationally expensive as the number of vector embeddings in the database grows.

To make this process more efficient, vector databases use approximate nearest neighbour (ANN) search algorithms. These algorithms trade off some accuracy for speed and are able to find an approximate set of nearest neighbours much faster than an exact search. They do this by creating an index, which makes use of storage structures that allow for efficient searching, such as trees or graphs. Some common ANN techniques are briefly outlined below:

• Hashing-based
  Locality-sensitive hashing (LSH) is a popular example of a hashing-based technique. These techniques work by using a number of hashing functions that aim to maximise hash collisions (two pieces of data sharing the same hash bucket), which differs from normal hashing where the aim is to minimise hash collisions. The collisions are maximised in such a way that similar vectors end up in the same hash buckets. At inference time a query vector is passed through the same hash functions, allowing similar vectors (vectors in the same hash bucket as the query vector) to be retrieved incredibly quickly. Whilst these techniques are very fast and can handle huge amounts of data, they are not very accurate. For a more rigorous explanation, see this guide.



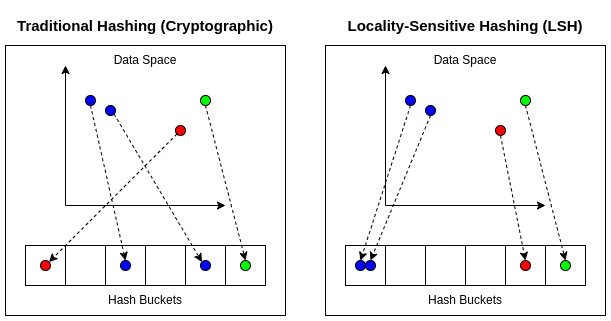
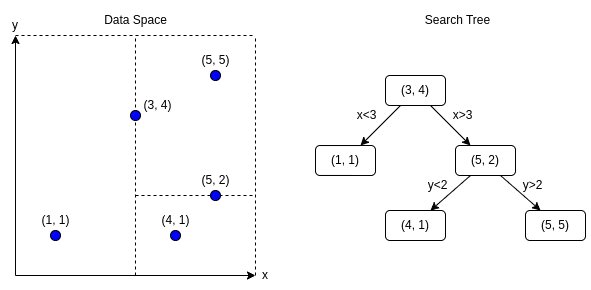
• Tree-based Spotify's Approximate Nearest Neighbours Oh Yeah (Annoy), as well as Sklearn's KDTrees are examples of tree-based algorithms. These methods construct a binary search tree (or collection of trees) whereby similar vectors are likely to end up in the same subtrees, which allows for a quick and efficient nearest neighbour search. The downside of tree-based indexes is that they perform reasonably well for low-dimensional data, but are not very accurate for high-dimensional data because they cannot adequately capture the complexity of the data.



• Inverted Index Based
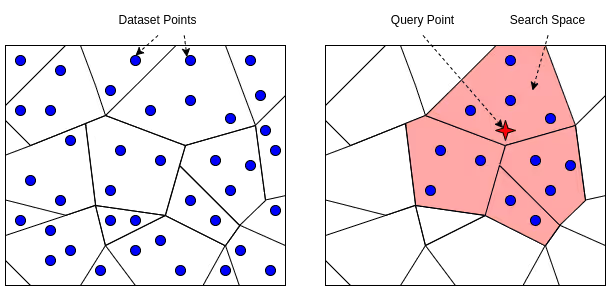
  Inverted File with Flat Compression (IVFFlat) is a common inverted index-based algorithm for ANN. This index is created by performing k-means to compute a number of centroids, which are then used to cluster the vectors into a number of cells (or buckets). These are illustrated in the Voronoi diagram on the left below. At inference time the nearest centroid, or centroids, are located, and then only those buckets need to be searched for nearest neighbours, vastly reducing the search space, as illustrated below on the right. IVFFlat has a relatively low build time and good filter performance, as it does not need to recalculate the entire index whenever a new vector is inserted. However, IVFFlat may suffer from poor query performance and increased latency compared to other algorithms, especially when dealing with high dimensional data.



• Graph-based
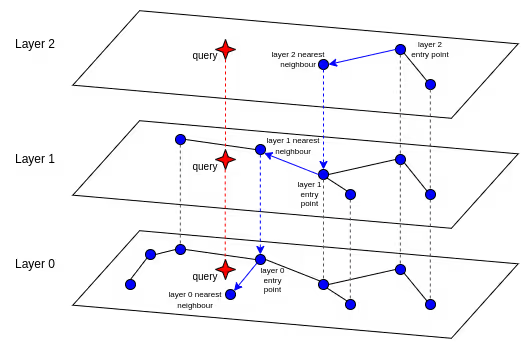
  Hierarchical Navigable Small World (HNSW) graphs are a very popular choice of ANN algorithm. They construct a hierarchy of graphs, whereby the high level graphs are fairly spread out, and the lowest-level sub-graphs connect the closest vectors together. This allows for a very efficient graph traversal during query time. This process is shown in the illustration below. HNSW offers excellent query performance and lower latency compared to IVFFlat. Its main drawback is the long build time required to generate the multi-layer graph structures. However, unlike IVFFlat, recall performance is unaffected by inserts, meaning the index doesn't need to be rebuilt after new data is inserted. There are also a number of graph-based techniques that allow for on-disk storage, vastly increasing the storage capacity of the ANN index, for example, Vamana.

3. Compression Techniques in Vector Databases

As we've explored various algorithms for efficient nearest neighbour search, it's important to address another critical challenge: managing the storage and computational demands of high-dimensional data. Embeddings generated by AI models can be large in both size and volume, especially when dealing with extensive datasets. This is where compression techniques come into play, offering solutions to reduce storage requirements and enhance query performance without significantly sacrificing accuracy.

High-dimensional vectors consume substantial storage space, which can quickly become a bottleneck as the number of embeddings grows. Moreover, the computational cost of processing these vectors during queries can lead to increased latency. Compression techniques help mitigate these issues by representing vectors in a more compact form, thereby reducing the storage footprint and speeding up similarity computations.

Several compression strategies are commonly employed in vector databases:

• Scalar Quantization: This method reduces the precision of each vector component by mapping continuous values to discrete levels. By using fewer bits to represent each dimension, scalar quantization decreases the overall size of the vector. While this can introduce minor quantization errors, it often provides a good balance between compression and accuracy.

• Product Quantization (PQ): PQ divides each vector into smaller sub-vectors and quantizes them independently using separate codebooks. This allows for an efficient approximation of distances between vectors directly in the compressed space. PQ is particularly effective because it enables a significant reduction in storage size while maintaining high query accuracy.

Implementing compression in vector databases offers several advantages. Firstly, compressed vectors take up less space, allowing databases to handle larger datasets without the need for proportional increases in storage infrastructure. Additionally, smaller vectors mean less data to process during similarity computations, leading to quicker query responses. Moreover, compression can enable more vectors to be loaded into memory, improving the efficiency of in-memory operations.

However, these benefits come with trade-offs. Compression can introduce errors due to the approximation of original vector values, potentially affecting the precision of similarity searches. Furthermore, some compression methods require additional processing to generate codebooks and encode vectors, which can lengthen the time needed to build or update indexes.

Many ANN algorithms are designed to work seamlessly with compression techniques. For example:

• IVF-PQ (Inverted File with Product Quantization): Combines inverted indexing with product quantization to efficiently narrow down candidate vectors and compute approximate distances in compressed space.

• HNSW with Compression: While HNSW graphs are powerful on their own, integrating compression can help manage memory consumption, especially for very large graphs.

By thoughtfully integrating compression, vector databases can achieve a desirable balance between performance, scalability, and accuracy.

3. Vector Databases In Action

As vector databases have become more popular, there are now a large number of open-source and commercial options available. Some of these plug into existing databases, such as various Postgres extensions, whilst others are standalone custom-built vector databases. Depending on your specific requirements, the option that best suits your needs vary.

Bearing in mind the trade-offs of build time, query time, recall, and storage capacity, it is worth doing some research to see which algorithms are supported by each database, and how they perform on your specific use case. This website provides a good overview of the vector database options currently available, and the ANN benchmarks project is a helpful resource for comparing the performance of different vector search algorithms.

Happy searching!