1. Introduction

One of the most important aspects of training a model is to determine the memory requirements for the training job. One approach is to start your training run, go for a beer, come back and see if it failed with an out of memory error. If it fails, make adjustments, rinse and repeat. Whilst this is perhaps a somewhat viable strategy, it is probably not the most efficient, and your beer expenditure may end up approaching your GPU training costs… Fortunately for us, there is another way!

In this guide, we will explore how to determine the memory requirements for a training job, specifically focussing on transformers. Broadly speaking, there are four main items that need to be stored in memory during the training of a neural network:

Model weights
Model gradients
Activations
Optimiser states

The first 3 items are all directly related to the architecture of the model itself. Varying layer widths, depths etc. as well as the floating point precision at which the tensors are stored, will affect the amount of memory required. These will be discussed in Architecture. The 4th item is more indirectly related to the model architecture. It is proportional to the number of parameters in the model, but the choice of optimiser itself will determine the relationship. This will be discussed in Optimiser.

There are some extra components that add a degree of uncertainty to the calculation of memory requirements, such as CUDA Kernels, buffers, intermediate results and memory fragmentation. CUDA Kernels typically require 1-2 GB of GPU memory, and buffers usually depend on your operating system. We are not going to delve into these in this guide, suffice to say they typically add a fairly constant, but somewhat unpredictable memory overhead.

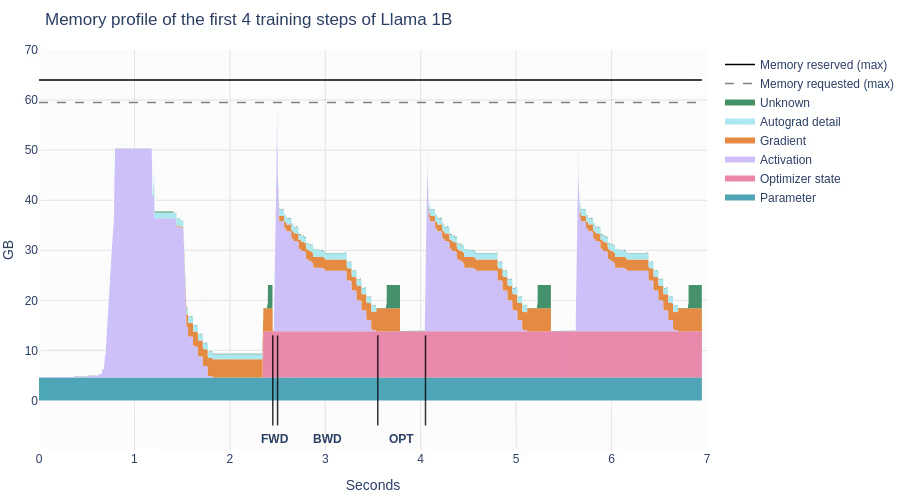
As a final note before we dive into things, it is worth noting that the memory requirements of a training job fluctuate quite significantly during the training process. Our job is to make sure we have enough memory to handle the peak memory requirements of the training run. The figure below shows the memory usage of the first 4 training steps of Llama 1B, taken using the PyTorch profiler. This figure comes from The Ultra-Scale Playbook: Training LLMs on GPU Clusters, an incredible book from the good people at Hugging Face, that this guide draws heavily from.

“Usage

2. Architecture

2.1 Model Weights and Gradients Memory

The memory requirements of a model’s weights and gradients are fairly straightforward to calculate. They are simply the number of parameters in the model, multiplied by the size of the floating point number used to store the parameters. This shouldn’t come as a surprise, as the weights are the parameters being stored, and each weight has a corresponding gradient that needs to be stored. (Note, there is some terminology abuse going on here, technically the parameters are not just the weights, but also the biases, and any other learnable parameters in the model, but researchers often use these terms interchangeably just to confuse us.)

For example, if we have a model with $N$ parameters, and we are using 32-bit floating-point (eg. FP32) numbers, each parameter will take 4 bytes (32 bits) to store. The memory requirements for the parameters ( $m_{param}$ ) and gradients ( $m_{grad}$ ) are simply:

\begin{aligned} m_{param} &= 4 \times N \text{ bytes} \\ m_{grad} &= 4 \times N \text{ bytes} \end{aligned}

2.1.1 Mixed Precision Training

In the above example, we can see that if we were to use 16-bit floating-point (eg. BF16) numbers, the memory requirements would be halved. However, in practice we usually can’t use lower precision numbers for the entire training process, due to numerical instability, which can stop the model from converging.

“Difference

To demonstrate this, consider what we are trading off when we move to lower precision numbers. We either reduce the number of bits used to represent the exponent, reducing the range of numbers that can be represented, or we reduce the number of bits used to represent the mantissa, reducing the precision of the number. The two figures below (again, from the The Ultra-Scale Playbook) illustrate this trade-off for various floating-point formats.

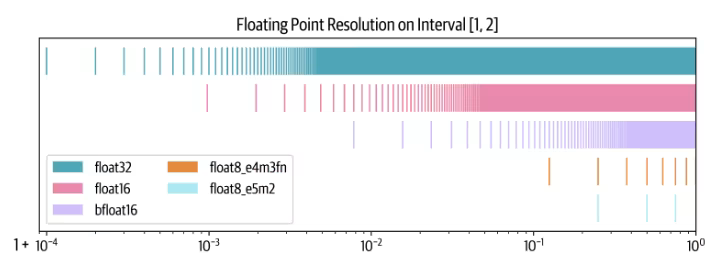
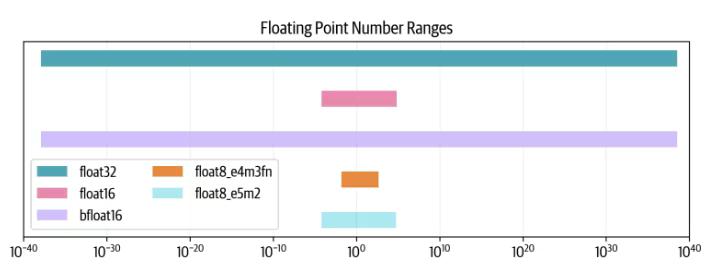
Why then bother with lower precision at all? The answer is that we can still benefit from using lower precision numbers for a lot of the training process, which increases the speed at which we can perform calculations, particularly on GPUs optimised for lower precision operations. This is known as mixed precision training, and usually involves doing most of the calculations in BF16, but keeping a master copy of the weights and gradients in FP32 for numerical stability. The memory requirements, therefore, are slightly increased compared to training without mixed precision:

\begin{aligned} m_{param} &= 2 \times N + 4 \times N \text{ bytes} \\ m_{grad} &= 2 \times N + 4 \times N \text{ bytes} \end{aligned}

As a final note on floating-points, there are some experimental training techniques that utilise even lower precision 8-bit floating-point numbers, which have been shown to reduce training memory requirements even further, but we will not go into these here.

2.2 Model Parameters

So far we have seen that our memory requirements all depend on the number of model parameters $N$ . The elephant in the room, is that we haven’t mentioned where this mysterious $N$ comes from. Fear not! We will now go through how to calculate $N$ step-by-step, using the GPT architecture as an example, loosely following this blogpost. A diagram of the architecture is shown below. For an awesome interactive 3-D visualisation of the transformer architecture, check out this.

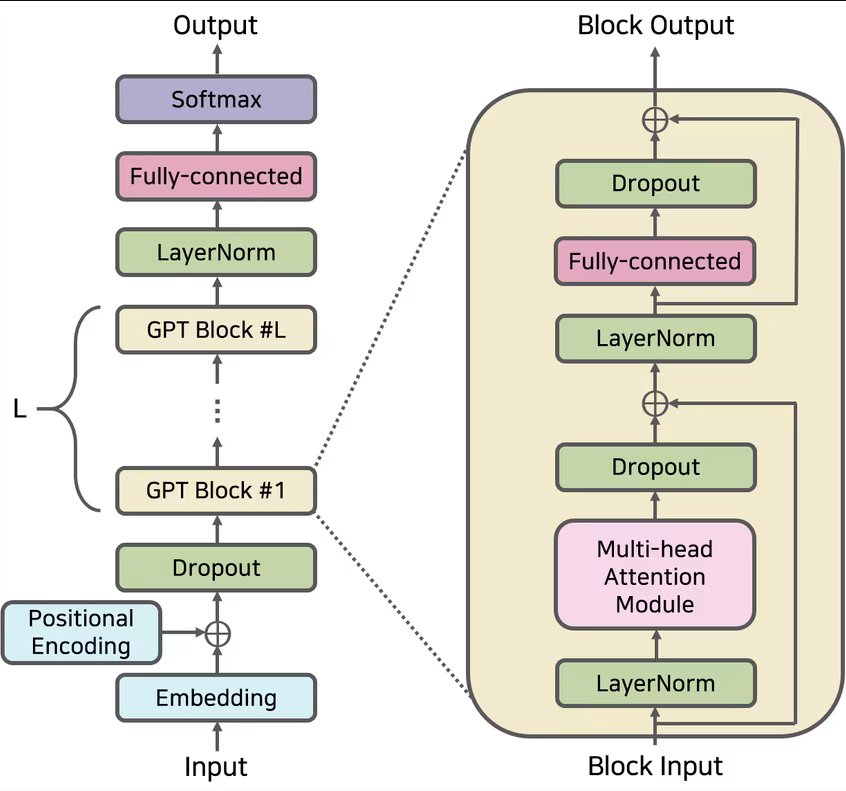
2.2.1 Input Layers

Embedding Layer

The very first layer of the model is the embedding layer. This layer takes the input tokens, and maps them to a high-dimensional vector space. The size of this vector space is simply the hidden dimension. The number of parameters in the embedding layer ( $N_{embed}$ ) is the product of the vocabulary size ( $v$ ) and the hidden dimension ( $h$ ):

N_{embed} = v \times h

Positional Encoding

Next we have the positional encoding layer. This layer adds positional information to the input tokens. The number of parameters in the positional encoding layer ( $N_{pos}$ ) is the product of the input sequence length ( $s$ ) and the hidden dimension ( $h$ ):

N_{pos} = s \times h

Note, in some architectures, the positional encoding is fixed and not learnt, so the number of parameters in this layer would be zero.

2.2.2 Transformer Layers

Layer Norm

The first layer in the transformer block is the layer norm. This layer performs normalisation of the input to the attention layer. The formula for layer norm is:

y = \frac{x - \mu}{\sigma} \times \gamma + \beta

Where $x$ is the input, $\mu$ is the mean, $\sigma$ is the standard deviation, $\gamma$ is the scale parameter and $\beta$ is the shift parameter. (Note, in practice there is usually a small epsilon term added to the denominator to avoid division by zero.)

The mean and standard deviation are calculated on the fly as the mean and standard deviation of the input $x$ , and so the only learnable parameters are $\gamma$ and $\beta$ , which are both vectors with the same dimension as the hidden dimension $h$ . Therefore, number of parameters in the layer norm layer ( $N_{ln}$ ) is simply:

N_{ln} = 2 \times h

There is a layer norm layer at the end of the transformer block as well, and so each layer norm contributes $2 \times N_{ln}$ parameters.

Attention Layer

This is where things get exciting, as the attention layer is the heart of the transformer architecture. First, we will describe single-head attention, then move onto multi-head attention. The attention function is calculated as:

\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^{T}}{\sqrt{d_{k}}}\right)V

Where $Q$ , $K$ and $V$ are the query, key and value matrices respectively, and $d_{k}$ is the dimension of the key matrix (which in the case of single-head attention is just the hidden dimension $h$ ). These key, query and value matrices are linear transformations of the input, and therefore each add a weight matrix of dimension $h \times h$ and a bias vector of dimension $h$ to the number of parameters. The number of parameters in the attention layer ( $N_{attn}$ ) is therefore:

N_{attn} = 3 \times h^{2} + 3 \times h

In the case of multi-head attention, the attention function is split across multiple heads that each transform the query, key and value matrices. This is illustrated in the figure below, where “h” represents the number of heads (not to be confused with $h$ the hidden dimension). To disambiguate, we will refer to the number of heads as $n_{heads}$ .

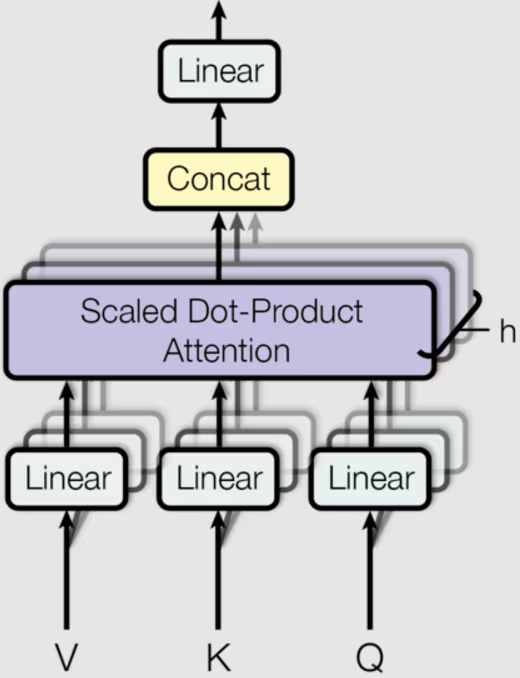
Multi-head attention is calculated as:

\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_{1}, \text{head}_{2}, \ldots, \text{head}_{n_{heads}})W^{O}

Where:

\text{head}_{i} = \text{Attention}(QW_{i}^{Q}, KW_{i}^{K}, VW_{i}^{V})

And $W_{i}^{Q} \in \mathbb{R}^{h \times d_{k}}$ , $W_{i}^{K} \in \mathbb{R}^{h \times d_{k}}$ , $W_{i}^{V} \in \mathbb{R}^{h \times d_{v}}$ and $W^{O} \in \mathbb{R}^{n_{heads} \cdot d_{v} \times h}$ . Usually $d_{k} = d_{v} = h/n_{heads}$ . For example if our hidden dimension $h = 768$ and we have $12$ attention heads, $d_{k}$ will be $768/12 = 64$ . Because of this, the number of parameters in the multi-head attention layer is very similar to the single-head case. To elaborate, in the multi-head case, we now have $n_{heads}$ times as many matrices, but each one is $\frac{1}{n_{heads}}$ times the dimension as before. The multi-head case does have the addition of an extra projection when the output of the attention heads is combined. That projection is simply a linear transformation again, and therefore in the multi-head case:

\begin{aligned} N_{attn} &= 3 \times h^{2} + 3 \times h + h^{2} + h \\ &= 4 (h^{2} + h) \end{aligned}

Dropout

You may have seen in the diagram above, that there is a dropout layer after the attention layer (as well as at other points in the architecture). The number of parameters added by dropout layers is zero, as dropout is a deterministic operation that doesn’t require any parameters.

Fully-Connected Layer

The final layer in the transformer block is the fully-connected layer, which is simply a feed-forward layer. This layer takes the output of the attention layer, and up projects it to a higher dimension, then reprojects it back to the hidden dimension.

It, therefore, adds two weight matrices, and two bias vectors, where the first weight and bias have dimensions $h \times d_{fc}$ and $d_{fc}$ , respectively, where $d_{fc}$ is the width of the fully-connected layer. Similarly, the second weight and bias have dimensions $d_{fc} \times h$ and $h$ , respectively. The number of parameters in the fully connected layer ( $N_{fc}$ ) is, therefore:

N_{fc} = 2 \times h \times d_{fc} + d_{fc} + h

You may sometimes see $d_{fc}$ rewritten as $4h$ , as it is often chosen to be $4$ times the hidden dimension, but we’ve chosen to keep the $d_{fc}$ term to make things more general.

2.2.3 Other Layers

The final layer in the model, after a series of these transformer blocks, is a final layer norm, which as previously discussed, adds $2 \times h$ parameters.

Depending on the task of the model, there may be some additional language modelling heads attached to the model, but for the purposes of keeping this guide general, we will ignore these.

2.2.4 Putting It Together

The total number of parameters in the model is the sum of the number of parameters in each of these layers we have discussed:

\begin{aligned} N &= N_{embed} + N_{pos} + L (N_{ln} + N_{attn} + N_{ln} + N_{fc}) + N_{ln} \\ &= vh + sh + L (2h + 4(h^{2} + h) + 2h + 2d_{fc}h + d_{fc} + h) + 2h \\ &= h(v + s) + L (4h^{2} + 9h + 2d_{fc}h + d_{fc}) + 2h \end{aligned}

Where $L$ is the number of transformer blocks in the model, and as a reminder, $h$ is the hidden dimension, $v$ is the vocabulary size, $s$ is the input sequence length, and $d_{fc}$ is the width of the fully-connected layer.

We can see from this formula, that the number of parameters is quite sensitive to the hidden dimension, as it scaled quadratically with $h$ . The number width of the fully-connected layers also has a significant impact on the number of parameters. As we’ve already mentioned, it is often a multiple of $h$ and so the $2d_{fc}h$ term can be rewritten as $2h^{2}c$ where $c$ is some constant, meaning this adds a multiplier to our quadratically scaling $h$ .

A very large vocabulary size, or input sequence length or both, can also significantly increase the number of parameters due to the $h(v + s)$ term, however, most of our parameters are still usually accounted for by the terms in the attention block, except in extreme cases. Where the input sequence length does have a big effect is in the memory requirements of the activations, which we will discuss next.

2.3 Activation Memory

What we refer to as activations, are the intermediate cached tensors used to efficiently compute chain rule derivatives during backpropagation. For a more detailed guide on activations and activation memory, check out this blog.

The activation memory requirements are a bit more difficult to calculate than the weights and gradients, as they depend on the size of the inputs to the model. Whilst the number of model parameters does have a small dependency on the input sequence length, the number of model parameters and, therefore, the weights and gradients memory is mostly independent of the inputs.

The formula for the memory requirements of the activations is:

m_{act} = L \cdot s \cdot bs \cdot h \cdot (34 + \frac{5 \cdot n_{heads} \cdot s}{h})

Where $L$ is the number of transformer blocks, $s$ is the input sequence length, $bs$ is the batch size, $h$ is the hidden dimension, and $n_{heads}$ is the number of attention heads. Deriving this is left as an exercise for the reader. Only joking, if you’re in the mood for more maths, you can find the derivation in Nvidia’s paper on activation recomputation.

What this equation tells us, is that the memory requirements of the activations are linearly proportional to the batch size and quadratically proportional to the sequence length. This means training on large batch sizes or very long input sequence lengths will cause the activation memory requirements to explode.

In fact, activation memory can often become the limiting factor in training memory requirements, as it can become much larger than the memory requirements of the weights and gradients. Fortunately, there are techniques that reduce this memory burden, such as activation recomputation/gradient checkpointing (recomputing some activations instead of storing them) and gradient accumulation (computing gradients iteratively in micro-batches).

3. Optimiser

The final piece of our training memory puzzle is the optimiser. Optimisers are responsible for improving training speeds, and ensuring model convergence, but require additional memory to store optimiser states. The memory requirements of the optimiser states are proportional to the number of parameters in the model, but the relationship is determined by the optimiser itself.

For example, the widely used Adam or AdamW optimisers store the momentum and variance in FP32 (4 bytes) for numerical stability, and so the memory requirements are:

m_{Adam} = 2 \times N \times 4 \text{ bytes}

Where $N$ is the number of parameters in the model. Other optimisers, such as Adafactor improve upon this by only storing aggregated information, and so the memory requirements are only 4 bytes per parameter:

m_{Adafactor} = N \times 4 \text{ bytes}

This comes at the cost of slower convergence, but can be a good trade-off if memory is a limiting factor.

The BitsAndBytes 8-bit Adam optimiser goes in a different direction. Instead of storing aggregates, it stores the full state, but quantises it down to 8-bit, reducing the memory requirements to 1 byte per parameter:

m_{8\text{-}bit Adam} = N \text{ bytes}

3.1 Multi-GPU Setups

So far this guide hasn’t really touched on multi-GPU training, but it is worth briefly mentioning that there are additional memory concerns when training on multiple GPUs. In the case of data parallelisation, we store the full model weights, gradients and optimiser states on each GPU (with each GPU copy simply receiving different subsets of the training dataset).

It turns out we don’t need to do this. Using DeepSpeed ZeRO (Zero Redundancy Optimiser), we can partition the optimiser states, gradients, and parameters across the data parallel dimension. This allows us to train models that usually wouldn’t fit into the memory of a single GPU. The figure below gives an overview of how the different ZeRO stages work.

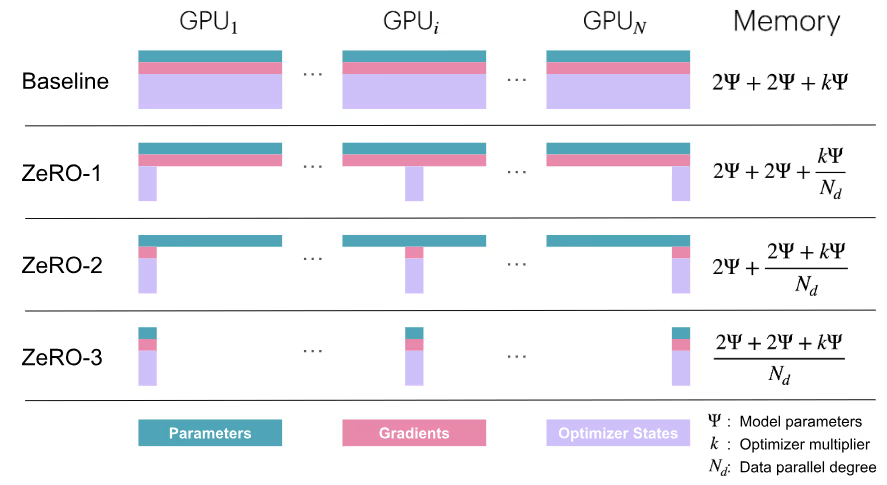
As with all things, there is no free lunch, and so ZeRO does come with some trade-offs. The main one being that the communication overhead between GPUs increases, as we need to communicate the parameters, gradients and optimiser states between GPUs. Luckily, this communication overhead is usually small.

Unfortunately, the activation memory requirements can’t be parallelised by ZeRO, and as we’ve seen, this is often one of the bigger memory needs. As mentioned before we can use techniques like activation recomputation and gradient accumulation to help handle this. More sophisticated parallelisation techniques like tensor parallelism can get around this limitation and allow us to shard the activations across GPUs as well. Beyond this, we can scale further by using techniques like context parallelism to train on very long input sequences, or pipeline parallelism to train very large model sizes, but these are beyond the scope of this guide.

4. Conclusion

Before we leave you in peace, let’s take a step back and consider what all of this amounts to. In recent history, we have seen a few trends in model development.

Firstly, we have seen the explosion of vocabulary sizes, with models being trained on thousands of unique tokens. When we think back to our memory usage formulae, it is easy to see why this is a good dimension to scale in. It causes a linear increase in memory (compared to the quadratic increases caused by hidden dimension and sequence length).

Secondly, we have seen various attempts at reducing the amount of caching needed in the attention layers. Instead of multi-head attention (MHA), we have seen methods like Grouped Query Attention (GQA) and Multi-Head Latent Attention (MLA) (introduced by DeepSeek-V3) which share the keys and values in various ways, reducing the memory burden caused by the attention layers.

Finally, on the vision-language side of things, there have been a few efforts to reduce the number of image tokens needed to represent an image, such as those described in Aya Vision and SigLIP 2. Whilst in some cases this has been driven by the desire to increase inference speed, it has the added benefit of reducing the memory requirements of training the model (if you remember, the activation memory requirements are quadratically proportional to the input sequence length).

The main takeaway here, is if you want to gamble on the future of where model development is going, understanding the fundamental formulae that govern the memory requirements of training large models is a good place to start. These formulae are governed by hard, physical limits, but if you can find clever ways to circumvent these limits, you can train models that are bigger, faster and more accurate than ever before.

Thank you for following along this journey. Hopefully you should have a good understanding of how varying various parameters of your model will affect your training memory requirements, as well as some techniques to reduce these requirements. Happy training!

Architecture & Optimising: Determining Training Memory